Suponga que el agua sale de un depósito por un orificio circular de área
en su fondo. Cuando el agua sale por el orificio, la fricción y la contracción de la corriente cerca del orificio reducen el volumen de agua que sale del depósito por segundo 
, donde c (0 < c < 1) es una constante empírica. Determine la ecuación diferencial para la altura h del agua en el instante t para el depósito que se muestra a continuación. El radio del orificio es de 2 pulg y g=32 |
Solución:
El volumen del agua en el tanque en el instante
t es 
Con esa ecuación podemos plantear una diferencia entre la altura y el tiempo en el que disminuye el volumen de agua en el recipiente:
=
Hemos conseguido una ecuación diferencial en base a los parámetros definidos planteada generalmente. Sin embargo, hay, a modo de condiciones iniciales unos valores que se pueden determinar para solucionar particularmente esta ecuación usando:
g = 32
Sustituyendo estos valores para las condiciones establecidas:
= 
Comportamiento de la ED para C=1
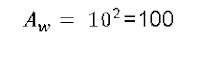
Perdona, pero no se ven bien las fórmulas.
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarmuchas gracias
ResponderEliminar